Complex Drawing
Polygon
const {polygon} = jscad.primitives;In einer der ersten 3D-Sessions, haben wir die 2D "Primitives" vorgestellt, wie rectangle und circle. Wenn wir darüber hinaus komplexere 2D-Formen zeichnen wollen, können wir die polygon-Funktion nutzen, die ähnlich wie die vertex Funktion in p5js funktioniert:
const poly = polygon({
points: [ // clockwise
[-10, -10],
[10, -10],
[10, 10],
[-10, 10],
[-10, -10],
]
});Das points-Attribut ist ein einfaches Array mit mehreren x/y-Punkt-Arrays. Wenn man später das Polygon extruden möchte, ist es sehr wichtig, dass die Punkte im Uhrzeigersinn sortiert sind.
Wir können auch Löcher in unser Polygon schneiden. Hierzu bauen wir ein weiteres Array um unsere Punkte und können dann weitere Polygone als Löcher hinzufügen. Wichtig: Löcher sind gegen den Uhrzeigersinn:
const poly = polygon({
points: [
[ // clockwise
[-10, -10],
[10, -10],
[10, 10],
[-10, 10],
[-10, -10],
],
[ // counter-clockwise
[-5, -5],
[-5, 5],
[5, 5],
[5, -5],
[-5, -5],
]
]
});Polyhedrons
const {polyhedron} = jscad.primitives;Die letzten 3D-Körper die wir uns noch anschauen sind die sogenannten Polyhedrons. Bevor wir aber damit anfangen, erst ein klein bisschen Therie dazu, wie 3D-Objekte eigentlich kunstruiert und gerendert werden. Falls du schon mal eine 3D-Software oder 3D-Objekte benutzt hast (z.B. in Computerspielen), ist dir vielleicht aufgefallen, dass wenn man ganz nah an Objekte herangeht, das die Oberflächen nicht glatt und rund sind, sondern aus vielen kleinen geometrischen Formen zusammengesetzt sind:

Selbst eigentlich runde Körper sind, wenn man sie genau betrachtet, aus Segementen aufgebaut. Heutzutage ist es schwieriger diese Unebenheiten zu entdecken, weil unsere Hard- und Software so leistungsstark geworden ist, dass extrem viele Segmente verarbeitet werden können, aber sie sind immer noch da. Auf der untersten Ebene sind eigentlich fast alle 3D-Körper aus ganz vielen Dreiecken aufgebaut (faces). Diese Dreiecke setzen sich aus Punkten (vertices) und den Kanten (edges) zwischen diesen zusammen.
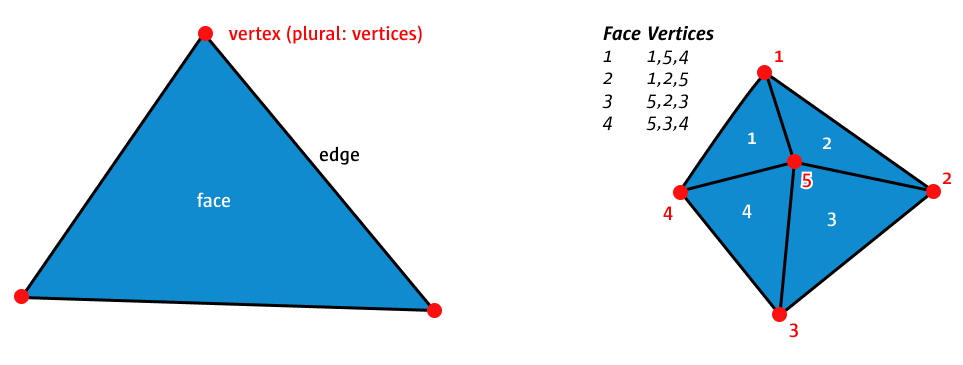
Warum Dreiecke? Dreiecke sind die einfachste Fläche. Eine Fäche die immer komplett "flach" ist. Durch das reine verschieben von Punkte, kann eine Dreiecksfläche nicht gebogen werden. Stell dir dazu ein Stück Papier vor. Wenn man ein Papierdreieck hat, kann man jede Ecke beliebig verschieben und die Fläche bleibt eben. Macht man das selbe mit einem Quadrat und bewegt nur eine Ecke, bildet sich eine Knickkante und wir haben zwei Dreiecke. Eine gerade Oberfläche zu haben ist wichtig, um z.B. effizient Reflektion, etc. zu berechenen, oder im Fall einer CNC-Fräse, bis wohin der Fräskopf fahren darf.
Wenn wir komplexe Objekte selber generieren wollen, müssen wir in Dreiecken denken, und wie wir diese Konstruieren können. Wir erstellen hierfür als erstes ein Araray mit Punkten, unseren vertices, den Eckpunkten unserer Dreiecke. Danach generieren wir eine Liste der Dreiecke und geben die Indices der Punkte an, welche wir benutzen wollen. Hier ein einfaches Beispiel mit nur einem Dreieck:
{
"points": [
[-10, -10, 0],
[10, -10, 0],
[10, 10, 0]
],
"faces": [
[0, 1, 2]
]
}Ein Quadrat aus zwei Dreiecken:
{
"points": [
[-10, -10, 0],
[10, -10, 0],
[10, 10, 0],
[-10, 10, 0]
],
"faces": [
[0, 1, 2],
[2, 3, 1]
]
}Wie man hier sieht, können wir die Punkte innerhalb unserer Punkt-Liste mehrfach verwenden. Anstatt 6 Punkte für zwei Dreiecke zu haben. Sind die 4 Eckpunkte unseres Quadrats ausreichend und wir können die Indices der Punkte einfach mehrfach nutzen. Dies ist nicht zwingend erforderlich, aber sauberer und effizienter. Folgende Variante generiert den selben Output:
{
"points": [
[-10, -10, 0],
[10, -10, 0],
[10, 10, 0],
[10, 10, 0],
[-10, 10, 0],
[-10, -10, 0]
],
"faces": [
[0, 1, 2],
[3, 4, 5]
]
}Wenn wir Punkte mehrfach in das Punkte-Array pushen, müssen wir aufpassen, dass es exakt die selben Punkte sind, anderenfalls hat unser Objekt später Löcher, was dann später in der Produktion zu Problemen führen kann.
Um das ganze noch komplizierter zu machen. Die Reihenfolge der Punkte innerhalb der Dreiecke muss im Uhrzeigersinn sein, wenn man von außen auf die Fläche darufschaut. :)
Das erstellen von Polyhedrons hat es in sich. Aber mit dieser Funktion kann man in Theorie jede erdenkliche Form generieren. Am besten fängt man solch ein Vorhaben immer damit an, erstmal eine Skizze zu machen und den Ablauf der Punkte und Dreiecke zu planen:
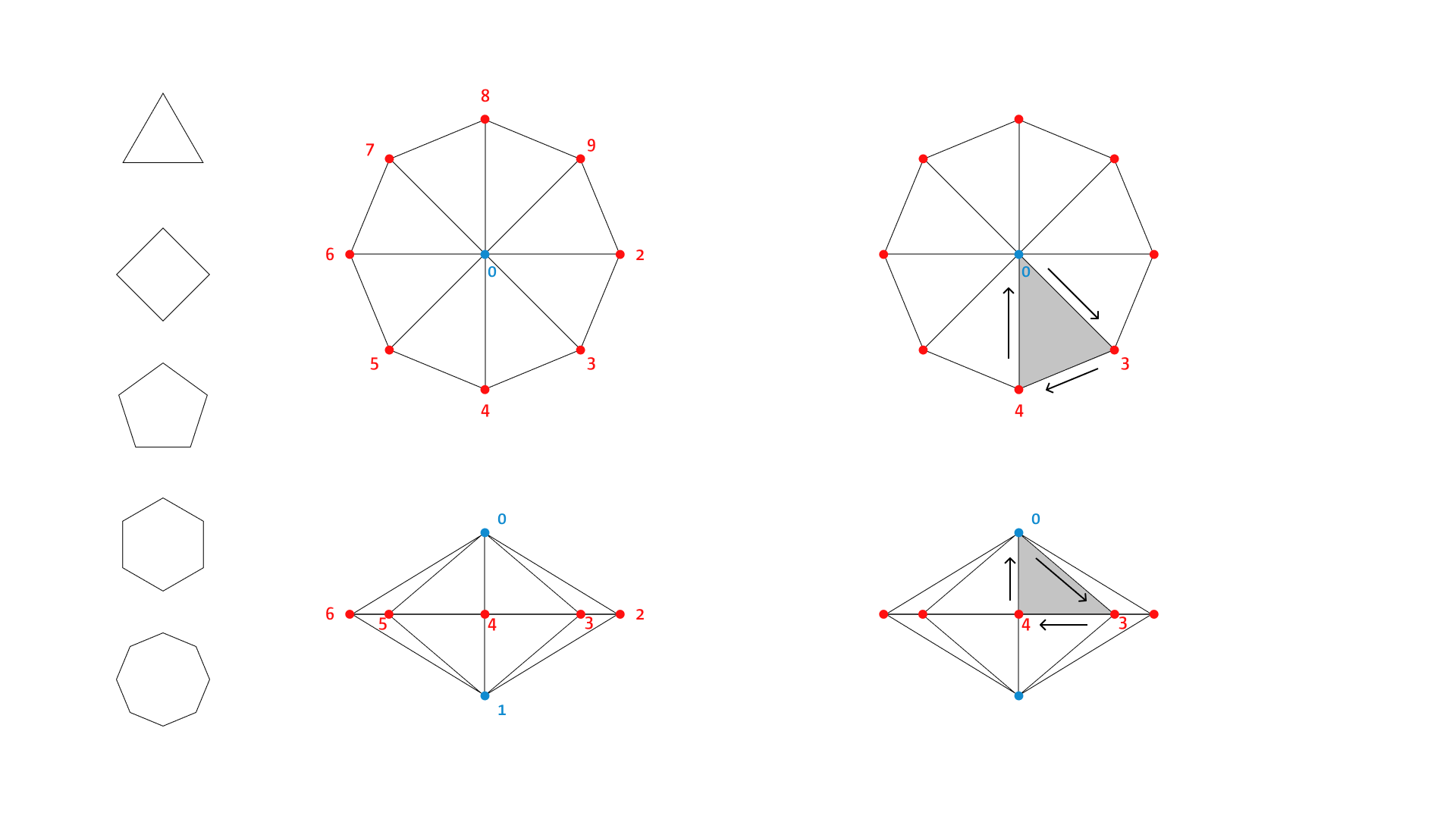
const jscad = require('@jscad/modeling');
const {polyhedron} = jscad.primitives;
function polar(radius, angle) {
const rad = Math.PI / 180 * angle;
const x = radius * Math.cos(rad);
const y = radius * Math.sin(rad);
return {x, y};
}
const main = () => {
const height = 50;
const top = [0, 0, height];
const bottom = [0, 0, -height];
const numPoints = 5;
const radius = 4;
const points = [top, bottom];
for (let p = 0; p < numPoints; p += 1) {
const point = polar(radius, 360 / numPoints * p);
points.push([point.x, point.y, 0]);
}
const faces = [];
for (let p = 0; p < numPoints; p += 1) {
// top
let p1 = p + 2;
let p2 = p + 3;
let p3 = 0;
if (p === numPoints - 1) {
p2 = 2;
}
faces.push([p1, p2, p3]);
// bottom
p3 = 1;
faces.push([p3, p2, p1]);
}
let shape = polyhedron({
points: points,
faces: faces,
orientation: 'outward'
});
return shape;
};
module.exports = { main };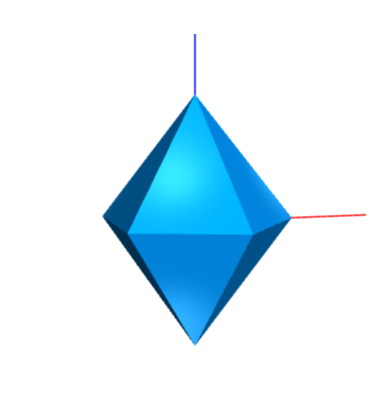
Aufgabe: Parametric Object
Erstelle einen 3D-Körper und nutze Parameter für die Größen- und Transformations-Angaben.
Inspiration: Daten-gestützte Oberfläche
Folgendes Beispiel ist von einer Arbeit des Büro nand.io inspiriert, die eine 3D-Daten-Visualisierung erstellt haben. Im folgenden Beispiel wird im Grunde ein dreidimensionales Area-Chart generiert. Schau dir den Code im Repo an und ändere z.B. die Werte im Daten-Array und beobachte wie sich die Visualisierung verändert.
Open "Daten-gestützte Oberfläche"

View on GitHub/lectures/3d/nand